Swing/FlatTreeNodeRoundedCornerSelection のバックアップ(No.1)

  • category: swing folder: FlatTreeNodeRoundedCornerSelection title: JTreeのノード選択で生成された直角多角形の角を丸める tags: [JTree, Path2D, Graphics] author: aterai pubdate: 2024-04-29T04:35:48+09:00 description: JTreeのノード選択で生成された直角多角形の角を尖点などが発生しないよう平坦化してから丸めます。 image: https://drive.google.com/uc?id=112_GkswNjQvzb1PwmPixbn2o2kw3VLgW

概要

JTreeのノード選択で生成された直角多角形の角を尖点などが発生しないよう平坦化してから丸めます。

Screenshot

screenshot

Download

サンプルコード

public static List<Point2D> flatteningStepsOnRightSide(
    List<Point2D> list, double arc) {
  int sz = list.size();
  for (int i = 0; i < sz; i++) {
    int i1 = (i + 1) % sz;
    int i2 = (i + 2) % sz;
    int i3 = (i + 3) % sz;
    Point2D pt0 = list.get(i);
    Point2D pt1 = list.get(i1);
    Point2D pt2 = list.get(i2);
    Point2D pt3 = list.get(i3);
    double dx1 = pt2.getX() - pt1.getX();
    if (Math.abs(dx1) > 1.0e-1 && Math.abs(dx1) < arc) {
      double max = Math.max(pt0.getX(), pt2.getX());
      replace(list, i, max, pt0.getY());
      replace(list, i1, max, pt1.getY());
      replace(list, i2, max, pt2.getY());
      replace(list, i3, max, pt3.getY());
    }
  }
  return list;
}

private static void replace(List<Point2D> list, int i, double x, double y) {
  list.remove(i);
  list.add(i, new Point2D.Double(x, y));
}
View in GitHub: Java, Kotlin

解説

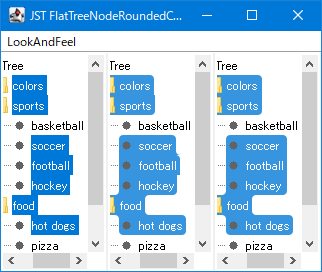
  • 左: デフォルトのJTree
    • TreeSelectionModel.DISCONTIGUOUS_TREE_SELECTIONでノードを複数範囲選択可能に設定
  • 中: ノード選択で生成された直角多角形の角を丸める
    • JListで作成したカレンダーのセル選択領域を角丸で描画すると同様の方法でノード選択の直角多角形の角を丸める
    • たとえばsoccer、football、hockeyノードを選択したときそのノード選択領域の直角多角形は右側に丸めのラウンド直径より幅が短い辺が生成されて、これを丸めるとスクリーンショットのように尖点やなめらかでない段差が発生してしまう
  • 右: ノード選択で生成された直角多角形のラウンド直径より短い辺を平坦化してから角を丸める
    • JTreeのノード選択から生成される直角多角形の場合、尖点になるような角は右側にのみ発生する可能性がある
      • このサンプルのJTreeではTree.leftChildIndentとTree.rightChildIndentの合計が丸めのラウンド直径より大きくなるので左側ではラウンド直径より短い辺は生成されない
    • 右側で丸めのラウンド直径より幅が短い辺を発見したら、その前後の角の座標を正方向に拡大するよう置換して平坦化
    • 平坦化を適用した直角多角形に「中」と同様の丸めを適用するのでsoccer、football、hockeyノードの選択領域の右辺は角がなくなり一直線になる

参考リンク

コメント